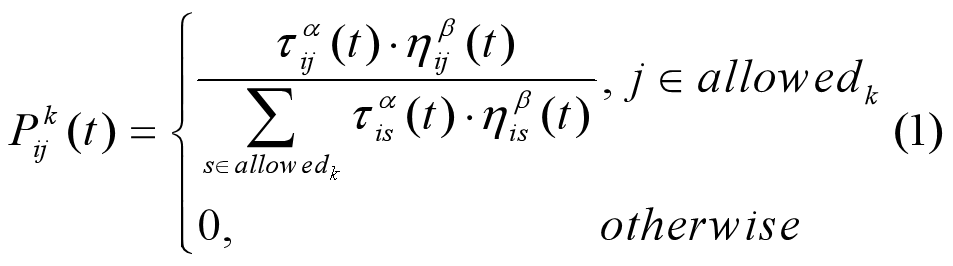智能优化算法 2：蚁群算法

基本原理

蚁群优化（ant colony optimization, ACO）算法是一种源自大自然生物世界的仿生类算法，其思想充分吸收了蚁群在觅食过程中的行为特性。

蚁群觅食，每只蚂蚁在经过的路上会留下一种化学物质，称为信息素，信息素会随着时间逐渐挥发，也就是说找到食物越慢，这条路上的信息素残留越少。其他蚂蚁可以感受到信息素的存在，并且能测量信息素的浓度。

通常蚂蚁会沿着信息素最浓的方向行走，毕竟是前人经验嘛，这样这条路上的信息素越来越浓；但偶尔也会突发奇想，试着走走信息素没那么浓，甚至没有信息素的路径，可能更快找到了食物。那么新路径信息素浓度很大，但也可能找不到食物，直到信息素挥发完毕。

如此反复，经过大量蚂蚁重复多次的探索，最终摸索出一条最短的路径；当然 不一定是全局最短，这点就不解释了。

数学模型

蚁群算法的基本迭代过程如下：

1. 初始化信息素：在所有路径上初始化一个较小的初始信息素值。
2. 每只蚂蚁构建路径：
   • 每只蚂蚁根据当前的信息素和启发式信息（如路径距离、时间等）选择路径，从起点到达终点。
   • 在路径选择过程中，蚂蚁会逐步走完整个路径，但此时并不会更新信息素。
3. 路径评估与信息素更新：
   • 在所有蚂蚁都走完路径后，收集每只蚂蚁的路径信息。
   • 计算每只蚂蚁在其路径上留下的信息素量​。
   • 叠加所有蚂蚁在每条路径上留下的信息素，更新全局信息素矩阵。
4. 挥发信息素：应用信息素挥发公式，使信息素浓度逐步减小，保持探索能力。

状态转移概率

这玩意决定了蚂蚁选择走哪条路。

• $P^k_{i,j}(t)$ 是状态转移概率，代表 t 时刻，第 k 只蚂蚁在 i 点选择往 j 点走的概率；
• allowed 表示蚂蚁 k 下一步允许选择的城市；
• $\tau_{ij}$ 表示 i，j 两点之间的信息素浓度
• $\alpha$ 是信息素启发因子，控制着 $\tau_{i,j}$ 对路径选择的影响程度：
  • 值越大，越依赖信息素，探索性降低；
  • 值越小，蚁群搜索的范围减少；
• $\eta_{ij}$ 表示 i，j 之间的能见度，反映了由 i 到 j 的启发程度，因此也叫启发函数
  • 通常取 i，j 距离 $d_{ij}$ 的倒数
  • 距离越短，启发函数值越大，因此表示蚂蚁在两点间转移的期望程度
• $\beta$ 是期望值启发因子，表示能见度的相对重要性，反映蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度：
  • 值越大，则状态转移概率越接近于贪心规则（距离越短我越走嘛）；

注意这里的 t 虽然译为“时刻”，但其实是迭代的次数，即 m 只蚂蚁全部走完一次后，才会加一。

信息素更新公式

初始化信息素浓度

$$\tau_{ij} = O$$

如果 O 太大，算法容易早熟，蚂蚁会很快的全部集中到一条局部最优的路径上。反之，如果 O 太小，信息素对搜索方向的指导作用太低，也会影响算法性能。

信息素更新规则

$$\tau_{ij}(t + 1) = (1 - \rho) \tau_{ij}(t) + \sum_{k=1}^{m} \Delta \tau_{ij}^k(t)$$

其中：

• $\tau_{ij}(t)$ 表示在时刻 t 路径 (i, j) 上的信息素浓度。
• $\rho$ 是信息素挥发系数，$0 < \rho < 1$。
  • 信息素随时间的衰减，能避免信息素无限累积，使得算法能不断探索新的路径，防止陷入局部最优。
• $\Delta \tau_{ij}^k(t)$ 是第 k 只蚂蚁在时刻 t 经过路径 (i, j) 时留下的信息素量，因此信息素增量是整个蚁群产生的增量。
  • 信息素的增量通常与路径的质量相关，路径越短（即质量越好），新增的信息素越多。

始终记得，在蚁群算法中，信息素更新是基于一次完整迭代中的所有蚂蚁行动结果进行的，而不是在每只蚂蚁行动之后立即更新。具体地说，公式中的 m 指的是当前迭代中参与路径构建的所有蚂蚁，即蚁群数量。

三种基本蚁群算法模型

$\Delta \tau_{ij}$ 的计算方法取决于具体的蚁群算法实现，常见的方法包括以下 3 种。这些模型的区别在于蚂蚁在路径上留下信息素的方式。

蚂蚁圈模型（Ant Cycle Model）

在蚂蚁圈模型中，信息素的更新发生在所有蚂蚁完成路径之后，综合每只蚂蚁的路径质量进行更新（全局更新）。这是最常用的蚂蚁算法模型。

其中 $\Delta \tau_{ij}^k$ 的一个常见的选择是：

$$\Delta \tau_{ij}^k = \begin{cases} \frac{Q}{L_k} & \text{如果蚂蚁 } k \text{ 经过了路径 } (i, j) \\ 0 & \text{否则} \end{cases}$$

其中 Q 是一个常数， $L_k$ 是第 k 只蚂蚁在本次迭代所走路径的总长度。

蚂蚁数量模型（Ant Quantity Model）

在蚂蚁数量模型中，蚂蚁在经过路径时留下的信息素为变量。属于局部更新，即信息素的更新是沿路径在每个节点处逐步进行的，而不是等所有蚂蚁完成路径后再统一更新。

$$\Delta \tau_{ij}^k = \begin{cases} \frac{Q}{d_{ij}} & \text{如果蚂蚁 } k \text{ 经过了路径 } (i, j) \\ 0 & \text{否则} \end{cases}$$

蚂蚁密度模型（Ant Density Model）

在蚂蚁数量模型中，蚂蚁在经过路径时留下的信息素为常量。属于局部更新。

$$\Delta \tau_{ij}^k = Q$$

Q 是一个常数。

蚁群算法求解 TSP 问题

旅行商问题，即 TSP 问题（Traveling Salesman Problem），给定一组城市和每对城市之间的距离，商家从其中一个城市出发，要求每个城市都要经过且只能经过一次，最后回到起点城市，求解商家访问这些城市的最短路径。

在经典的 TSP 中，假设所有城市之间都存在路径，即形成一个完全图。也就是说，每对城市之间都有直接的边连接。

完整代码