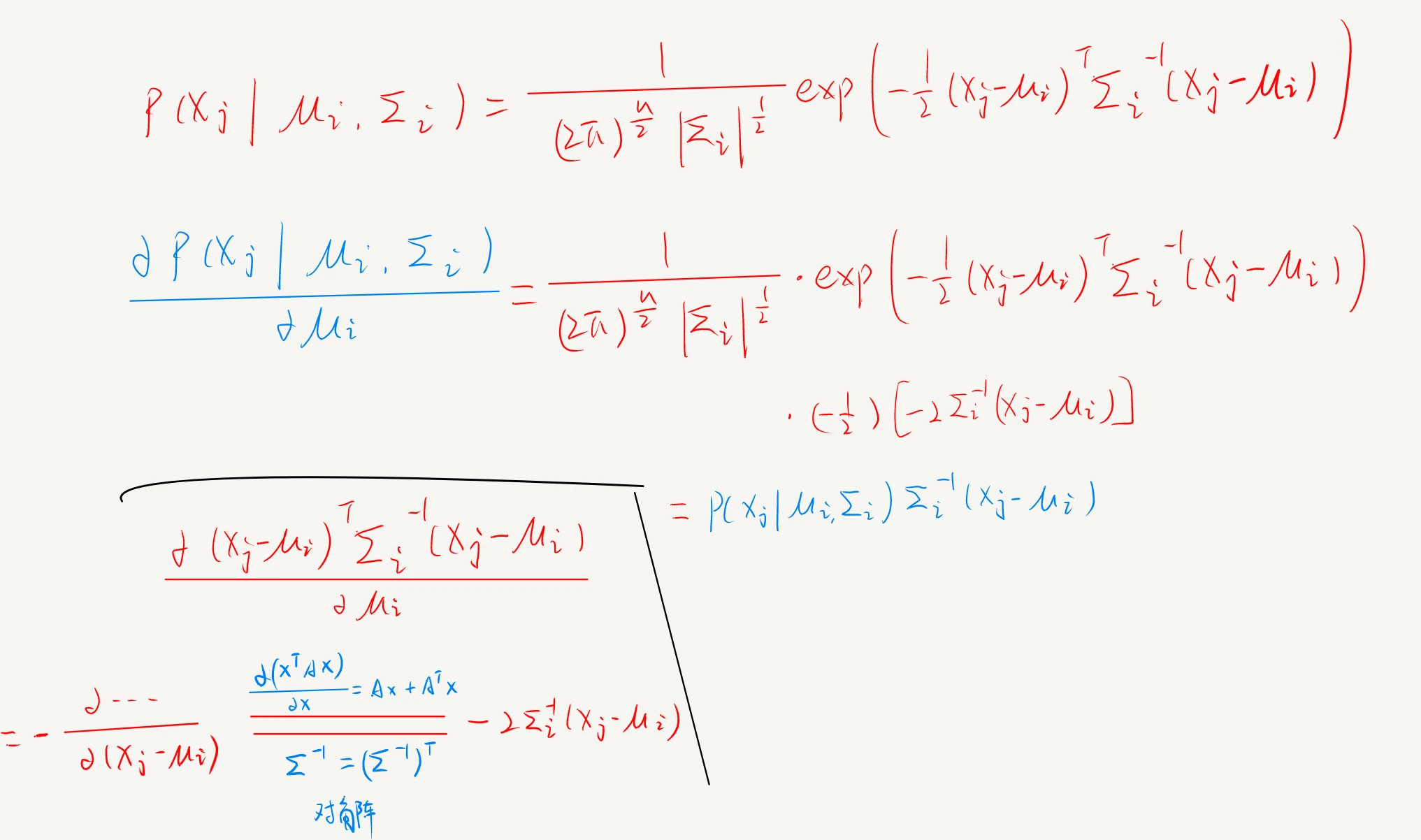第四阶段:
聚类及常用聚类算法
要求:了解什么是聚类?聚类的无监督性,熟悉常见的聚类算法,明确其在适用场景及作用,自选实例搭建模型开展实验并给出结论。提交研学材料包括(研学笔记,实例源码,模型实验讲解视频)(3周)
机器学习:聚类算法与无监督学习、模型评估标准-阿里云开发者社区
https://developer.aliyun.com/article/1142803
聚类的任务
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个 “簇” (cluster)。通过这样的划分,每个簇可能对应于一些潜在的概念 (类别),如 “浅色瓜” “深色瓜”,“有籽瓜” “无籽瓜”,甚至 “本地瓜”“外地瓜”等。
需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇所对应的概念语义需由使用者来把握和命名。
性能度量
聚类性能度量也称为聚类有效性指标(validity index),顾名思义,是用来衡量聚类效果的好坏的。
那么,什么样的聚类结果算好呢?俗话说“物以类聚”,在聚类时,我们希望同一簇(同一类)的样本尽可能聚集在一起,而不同簇(不同类)的样本最好远远地隔开,甚至是完全不重合(即没有交集)。这两种情况我们分别用聚类结果的簇内相似度和簇间相似度来描述,即“簇内相似度高,簇间相似度低”。
K-Means 算法

均值向量 μ 的计算方式:
μi=Ci1x∈Ci∑x,i=1,...,k
样本与各均值向量 μi 的距离 dji 使用 Lp 范数,这里使用的是 L2 范数。
学习向量量化
学习向量量化,Learning Vector Quantization,简称 LVQ。与 k-means 类似, LV Q 也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是, LVQ 假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。

上述算法中,关键是原型向量的更新。
-
如果最近的原型向量 pi∗ 与 xj 的类别标记相同(即认为样本 xj 属于簇 Ci ),则令 pi∗ 向 xj 的方向靠拢,此时新的原型向量 p′ 为
p′=pi∗+η⋅(xj−pi∗)
则 p′ 与 xj 的距离为
∣∣p′−xj∣∣2=∣∣pi∗+η⋅(xj−pi∗)−xj∣∣2=(1−η)⋅∣∣pi∗−xj∣∣2
也就是原型向量 pi∗ 在更新为 p′ 后,将会更加接近 xj
因为在旧的距离上乘了 1−η , η∈(0,1) 是学习率
-
如果最近的原型向量 pi∗ 与 xj 的类别标记不同,那说明聚类得到的簇不对,那就应该让更新后的原型向量远离样本 xj
p′=pi∗−η⋅(xj−pi∗)
同理,也可以推出
∣∣p′−xj∣∣2=(1+η)⋅∣∣pi∗−xj∣∣2
也就是让更新后的原型向量 p′ 与 xj 的距离变大的意思。
通过上面这种方法,我们可以学得一组原型向量 {p1,p2,...,pq} ,这些向量就能够构建出一个对样本空间 X 的簇划分。对于每个原型向量 pi ,它定义了一个与之相关的区域 Ri :
Ri={x∈X∣∣∣x−pi∣∣2≤∣∣x−pi′∣∣2,i′=i}
也就是区域 Ri 中的每个样本 x 到 pi 的距离,都是不超过其他的原型向量和 x 之间的距离的。换言之,这么多的区域 R ,你 x 离我 Ri 是最近的,那你当然是属于我所代表的这个簇的样本,而不是其他的什么簇。
这样形成的对样本空间 X 的簇划分 {R1,R2,...,Rq} ,成为“Voronoi 剖分”。
高斯混合聚类
概率密度
多元高斯分布的概率密度函数为
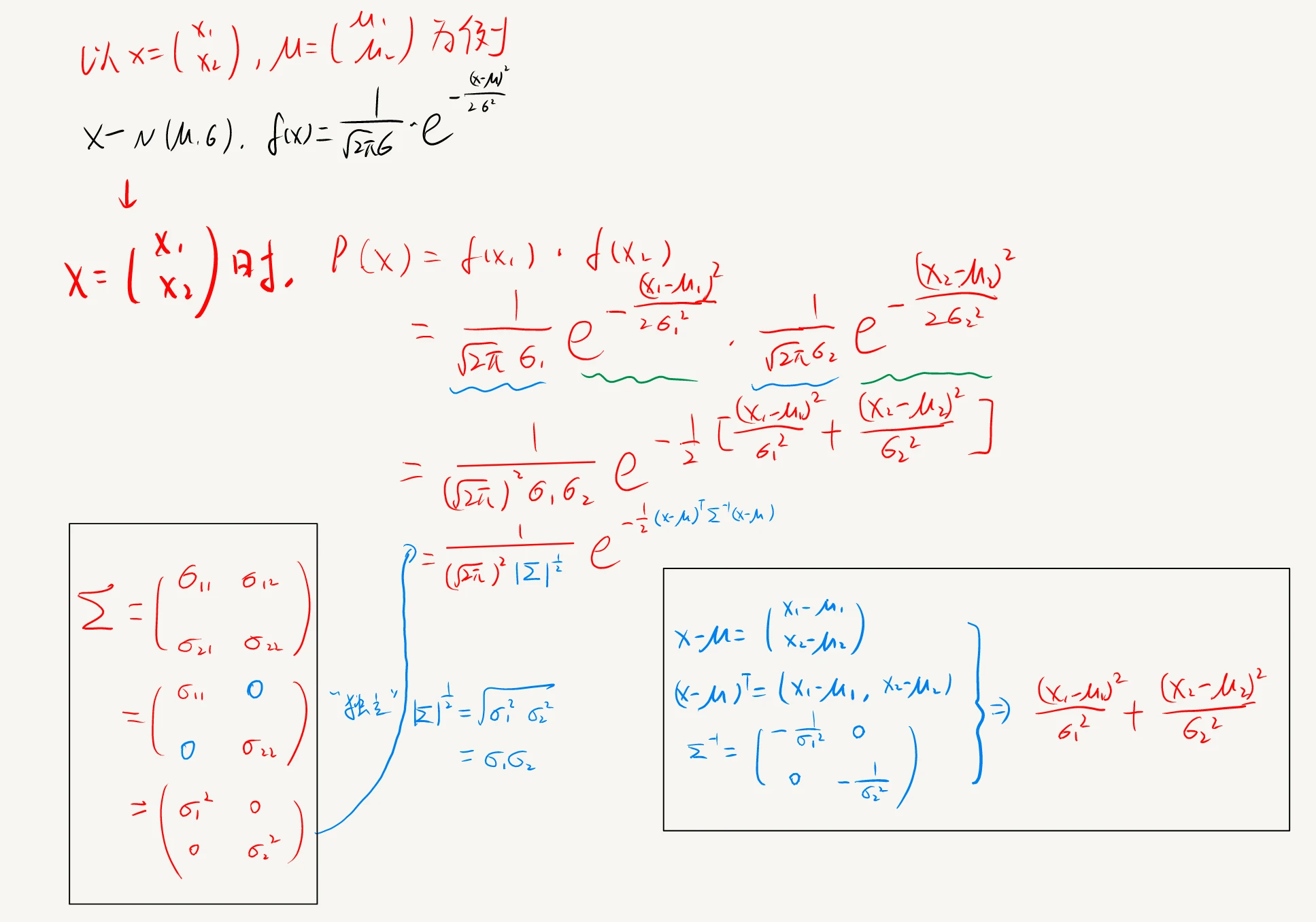
p(x)=(2π)2n∣Σ∣211e−21(x−μ)TΣ−1(x−μ)
其中, μ 是 n 维均值向量, Σ 是 nxn 的协方差矩阵。其推导过程如下:

协方差矩阵反应的是各元素之间的相关性(正、负 or 零)。而这里我们的实际情况显然是离散的随机变量,因此属于独立分布,即相关性为 0,故对应维度的协方差矩阵的元素也为 0
为了明确显示高斯分布和相应参数的关系,可以将 p(x) 记作 p(x∣μ,Σ)
知道这三个玩意都是向量和矩阵就行了,我懒得打加粗显示了。。。麻烦
高斯混合分布
接下来,定义高斯混合分布:
pM(x)=i=1∑kαi⋅p(x∣μi,Σi)
- k 指的是有 k 个高斯分布组成了一个高斯混合分布,其中每一个高斯分布叫做“混合成分”
- μi 和 Σi 是第 i 个高斯分布(在这里叫做高斯混合成分)的参数
- αi 叫做“混合系数”。假设样本是通过一个高斯混合分布产生的,那么 αi 的意思是选择第 i 个混合成分的概率,类似于“初始概率分布”的意思
高斯混合分布其实就是对组成它的每个高斯分布,乘了一个概率分布 α ,然后把它们加起来
后验概率
现在,假设训练集 D={x1,x2,...,xm} 就是通过上面说的高斯混合分布生成的,假设**样本 xj 属于的那个高斯混合成分记作 zj ** ,那么有
pM(zj=i∣xj)=pM(xj)p(zj=i)⋅pM(xj∣zj=i)
先不用纠结这个式子是什么含义,只从等式的结构上看,它成立的依据是贝叶斯定理。其实你把分子乘过去的话,等号两边的两个乘式,结果都是 p(zj=i,xj)
不要去纠结 p 和 pM 怎么乘。它俩就是个符号,表示的都是概率,也就是一个数字而已。
再来看 pM(zj=i∣xj) ,它给出的是样本 xj 由第 i 个高斯混合成分生成的后验概率,或者读作“已知一个样本 xj ,它属于第 i 个高斯混合成分的概率是多少 ”。所以不要在意为啥又多了一个符号 z ,其实没啥卵用,只是这帮数学家为了表示方便,引入的一个新符号而已 hhh。
那么这个后验概率等于多少呢?来处理一下等式右边的部分就知道了。我们先把上文定义的高斯混合分布那一堆东西给代入进来
p(zj=i)pM(xj∣zj=i)pM(xj)=αi=p(xj∣μi,Σi)=l=1∑kαl⋅p(xj∣μl,Σl)
第一个式子很简单,咱们定义的 αi 本来就是这个概率的含义。第三个式子就是上面的高斯混合分布定义照抄下来的,只是原式里的符号 i ,在这里有具体的含义,即第 i 个高斯混合成分,因此给它换了个符号 l 而已。
有人或许会疑惑第二个式子为什么成立。第二个式子的左式,表示的是在“第 i 个高斯混合成分里取一个样本 xj 的概率”,那对应的不就是第 i 个高斯混合成分的概率密度函数,即 p(xj∣μi,Σi) 吗?
然后把这三个等式,替换到后验概率的式子中,得到
pM(zj=i∣xj)=pM(xj)p(zj=i)⋅pM(xj∣zj=i)=∑l=1kαl⋅p(xj∣μl,Σl)αi⋅p(xj∣μi,Σi)
然后,天才的(holy shit)数学家们觉得 pM(zj=i∣xj) 长得也太复杂了,于是把它记作 γji(i=1,2,...,k)
默默地在心里背诵三遍, γji 就是 pM(zj=i∣xj) ,就是已知一个样本 xj ,它属于第 i 个高斯混合成分的概率是多少
簇标记
回归正题,我们的主题是聚类算法,所以结果是要找到样本对应的簇标记,然后划分到不同的簇中。那么如何确定样本 xj 的簇标记呢?显然, xj 属于哪个高斯混合成分的概率最大,自然就是属于这个类的,也就可以得到簇标记了,即
λj=i∈{1,2,...,k}argmaxγji
所以为什么说高斯混合聚类也是属于原型聚类。相比于 k-means 和 LVQ 使用 Lp 范数,GMM 采用的是概率模型对原型进行刻画。也就是从“谁离得更近”,变成了“谁最有可能”。
EM 算法求解
现在,我们知道要解决的问题就是上面这个找最大的 γ 。还记得上面背诵三遍的东西吗
γji=pM(zj=i∣xj)=∑l=1kαl⋅p(xj∣μl,Σl)αi⋅p(xj∣μi,Σi)
显然,这个式子跟三个东西有关,即 {α,μ,Σ} ,因此用 EM 算法进行迭代优化求解。
首选取对数似然函数,
LL(D)=ln(j=1∏mpM(xj))=j=1∑mln(i=1∑kαi⋅p(xj∣μi,Σi))
对 μ,Σ 分别求偏导并令其为 0,可解得
μi=∑j=1mγji∑j=1mγjixj
Σi=∑j=1mγji∑j=1mγji(xj−μi)(xj−μi)T
这里先给出一部分 μ 的证明,因为链式求导也就只有这一个难点,至于 Σ 就随缘吧 hhh。关于矩阵求导的问题,见矩阵求导的推导 2.3 部分。
这一段“南瓜书”中的矩阵求导法则说法貌似有点小小的不严谨?书里给的直接是 2Ax,但这里只不过对角阵正好满足 AT=A ,所以是 2Ax

对于 α ,除了要求偏导,还需要满足其自身的条件,即 αi≥0,∑i=1kαi=1 ,因此要用拉格朗日乘数法,解得(证明略)
αi=m1j=1∑mγji
算法综述

基于密度的聚类方法 (DBSCAN)
定义
密度聚类也称“基于密度的聚类”(density-based clustering),顾名思义,此类算法根据样本分布的紧密结构,来进行类别划分。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种著名的密度聚类算法,它基于一组“邻域”参数 (ϵ,MinPts) 来刻画样本分布的紧密程度 。
给定数据集 D={x1,x2,...,xm} ,定义如下概念
-
ϵ - 邻域: Nϵ(xj)={xj∈D∣dist(xi,xj)≤ϵ}
对于一个样本 xj ,我们可以计算出其他样本点到 xj 的距离 dist ,这个距离默认情况下设为欧氏距离。然后我们给定一个 ϵ 参数,表示一个距离限度值,如果 dist 大于这个值,就认为该样本距离 xj 太远了,所以不计入邻域;反之,小于等于 ϵ ,就将该样本放入 Nϵ(xj)
-
核心对象:若 xj 的 ϵ - 邻域至少包含 MinPts (min+points:最少样本点数)个样本,即 ∣Nϵ(xj)∣≥MinPts ,则 xj 是一个核心对象
也就是说,想成为核心对象,首先周围要有一堆样本。这堆样本要满足两个条件:一是到你的距离得足够近,小于 ϵ ;二是数量要够,至少得 MinPts 个。
- 密度直达(直接密度可达):若 xj 在 xi 的 ϵ - 邻域中,且 xi 是核心对象,则称 xj 由 xi 密度直达
显然,密度直达在默认条件下是不满足对称性的,即 xj 由 xi 密度直达时, xi 不一定由 xj 密度直达。但如果 xi,xj 都是核心对象,那么密度直达就满足对称性。
- 密度可达:对 xi,xj ,若存在样本序列 p1,p2,...,pn ,其中 p1=xi,pn=xj ,且 pi+1 由 pi 密度直达,则称 xj 由 xi 密度可达
对于样本序列{P}, pi+1 由 pi 密度直达,也就是后一项由前一项密度直达,这意味着 p1,p2,...,pn−1 都是核心对象( pn 不一定是 ),且相邻两项的距离小于 ϵ
密度可达在核心对象间也是满足对称性的。
- 密度相连:对 xi,xj ,若存在 xk 使得 xi,xj 均由 xk 密度可达,则称 xi 与 xj 密度相连

图中红色为核心对象,绿色为密度可达。两个绿色之间为密度相连。
DBSCAN 算法
基于上述概念,DBSCAN 要找的簇,就是由 x 密度可达的所有样本组成的集合。

\ 表示求差集
具体代码见 https://github.com/sun2ot/python-study/blob/main/clustering/dbscan.py
层次聚类
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略,也可采用 “自顶向下”的分拆策略。
AGENS 是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中每个样本看做一个单独的聚类簇,然后在算法中每一步都寻找距离最近的两个聚类簇合并,重复该过程,直到达到预设的聚类簇个数。
集合间的距离
AGENS 算法的重点在于如何计算集合的距离。通常情况下,采用豪斯多夫距离(Hausdorff distance):
对于同一样本空间中的集合 X 和 Z ,
distH(X,Z)=max(disth(X,Z),disth(Z,X))
其中,
disth(X,Z)=x∈Xmaxz∈Zmin∣∣x−z∣∣2
关于豪斯多夫距离
也可以用以下式子来计算距离
最小距离:
dmin(Ci,Cj)=x∈Ci,z∈Cjmindist(x,z)
最大距离:
dmax(Ci,Cj)=x∈Ci,z∈Cjmaxdist(x,z)
平均距离:
davg(Ci,Cj)=∣Ci∣∣Cj∣1x∈Ci∑z∈Cj∑dist(x,z)
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定, 而平均距离则由两个簇的所有样本共同决定。
AGENS 算法

https://github.com/sun2ot/python-study/blob/main/clustering/agnes.py
附录