完整可执行代码见 sun2ot/algorithm-learning

基本思想

分支限界法类似于回溯法，也是在问题的解空间上搜索问题解的算法。一般情况下，分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出解空间中满足约束条件的所有解，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解，即在某种意义下的最优解。

由于求解目标不同，导致分支限界法与回溯法对解空间的搜索方式也不相同。回溯法以深度优先的方式搜索解空间，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间。

分支限界法的搜索策略是，在扩展结点处，先生成其所有的儿子结点（分支），然后再从当前的活结点表中选择下一个扩展结点。为了有效地选择下一扩展结点，加速搜索的进程，在每一活结点处，计算一个函数值（限界），并根据函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间上有最优解的分支推进，以便尽快地找出一个最优解。这种方法称为分支限界法。

在搜索问题的解空间树时，分支限界法与回溯法的主要区别在于它们对当前扩展结点所采用的扩展方式不同。在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

从活结点表中选择下一扩展结点的不同方式导致不同的分支限界法。最常见的有以下两种方式:

  1. 队列式(FIFO)分支限界法：队列式分支限界法将活结点表组织成一个队列，并按队列的先进先出原则选取下一个结点为当前扩展结点。
  2. 优先队列式分支限界法：优先队列式的分支限界法将活结点表组织成一个优先队列，并按优先队列中规定的结点优先级选取优先级最高的下一个结点成为当前扩展结点。

布线问题

问题定义

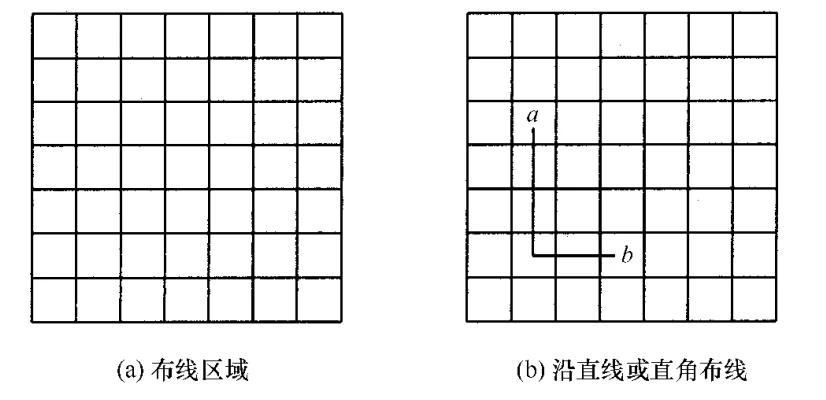
印刷电路板将布线区域划分成 n×mn\times m 个方格阵列，如图(a)所示。精确的电路布线问题要求确定连接方格 a 的中点到方格 b 的中点的最短布线方案。在布线时，电路只能沿直线或直角布线，如图(b)所示。为了避免线路相交，已布了线的方格做了封锁标记，其他线路不允许穿过被封锁的方格。

image.png|300*400

算法思想

布线问题的解空间是一个图。解此问题的队列式分支限界法从起始位置 a 开始将它作为第一个扩展结点。与该扩展结点相邻并且可达的方格成为可行结点被加入到活结点队列中，并且将这些方格标记为1，即从起始方格 a 到这些方格的距离为1。接着，从活结点队列中取出队首结点作为下一个扩展结点，并将与当前扩展结点相邻且未标记过的方格标记为2，并存入活结点队列。这个过程一直继续到算法搜索到目标方格 b 或活结点队列为空时为止。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#define LENGTH 6  // 网格的边长
#define MAX_LENGTH (LENGTH + 2)  // 网格的边长加上边界

int grid[MAX_LENGTH][MAX_LENGTH];  // 网格

typedef struct {  // 网格位置
    int row, col;
} Position;

/**
 * 在给定的起点和终点之间查找路径。
 *
 * @param start 起点位置
 * @param finish 终点位置
 * @param PathLen 路径长度的指针
 * @param path 路径的指针
 * @return 如果找到路径，则返回true；否则返回false。
 */
bool FindPath(Position start, Position finish, int *PathLen, Position **path) {
    Position nextStep[4] = {
        {0, 1},  // 右
        {1, 0},  // 下
        {0, -1}, // 左
        {-1, 0}  // 上
    };

    Position here, next;  // 当前位置和下一个位置
    // 将起点位置赋值给当前位置
    here.row = start.row;  
    here.col = start.col;
    grid[start.row][start.col] = 1;  // 起始点置为1表示已访问
    Queue Q;
    initQueue(&Q);

    while (true) {
        for (int i = 0; i < 4; i++) {  // 检查当前位置的四个方向
            // 四次循环分别检查右、下、左、上四个方向
            next.row = here.row + nextStep[i].row;  
            next.col = here.col + nextStep[i].col;
            // 该位置未被访问过且不是障碍物/边界
            if (grid[next.row][next.col] == 0 && next.row != -1 && next.col != -1) {  
                grid[next.row][next.col] = grid[here.row][here.col] + 1;  // 更新到达该位置的路径长度
                if (next.row == finish.row && next.col == finish.col)   // 到达目标终点
                    break;

                enqueue(&Q, next);  // 将新探测的布线位置(活结点)入队
            }
        }

        if (next.row == finish.row && next.col == finish.col)   // 对于目标终点，不再探测
            break;
        if (isEmpty(&Q)) return false;  // 队列为空，说明没有路径

        here = dequeue(&Q);  // 取出队首元素，作为新的当前位置
    }

    *PathLen = grid[finish.row][finish.col];  // grid终点存储了到达此处的路径长度
    *path = (Position *)malloc(*PathLen * sizeof(Position));  // 分配存储路径轨迹的空间
    here = finish;  // 从终点开始回溯

    for (int j = *PathLen - 1; j >= 0; j--) {  
        (*path)[j] = here;  // 将当前位置存入路径轨迹
        for (int i = 0; i < 4; i++) {  // 检查当前位置的四个方向
            next.row = here.row + nextStep[i].row;  
            next.col = here.col + nextStep[i].col;
            // 回溯时路径长度j逐渐减小，因此若当前位置四周有路径长度为j的点，则说明是上一个点
            if (grid[next.row][next.col] == j)  
                break;
        }
        here = next;  // 将回溯的点作为新的当前位置
    }

    return true;
}

关于 grid 的论述

grid 数组存储了到达当前位置的最短路径长度。

  • 为 -1 时，由于不可能存在比它更小的值，因此作为边界/障碍物使用
  • 为 0 时，表示尚未记录到达此处的距离，因为表示该点没有被访问过
  • 为 >0 的值时，表示到达此处的当前最短距离。