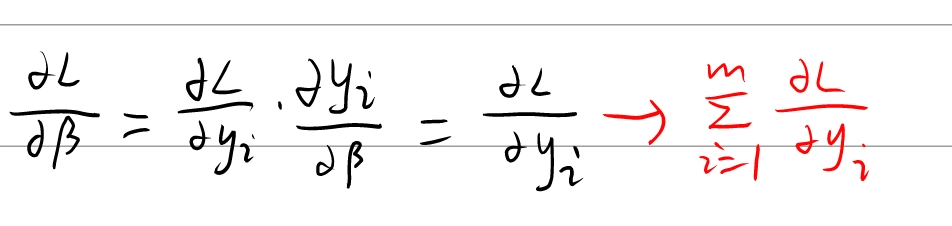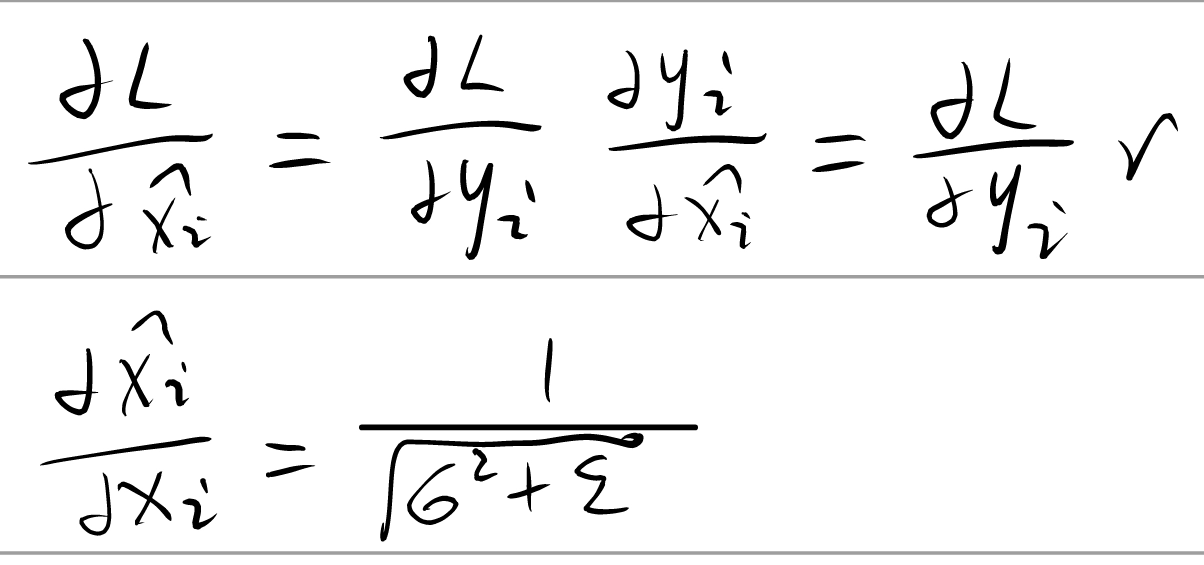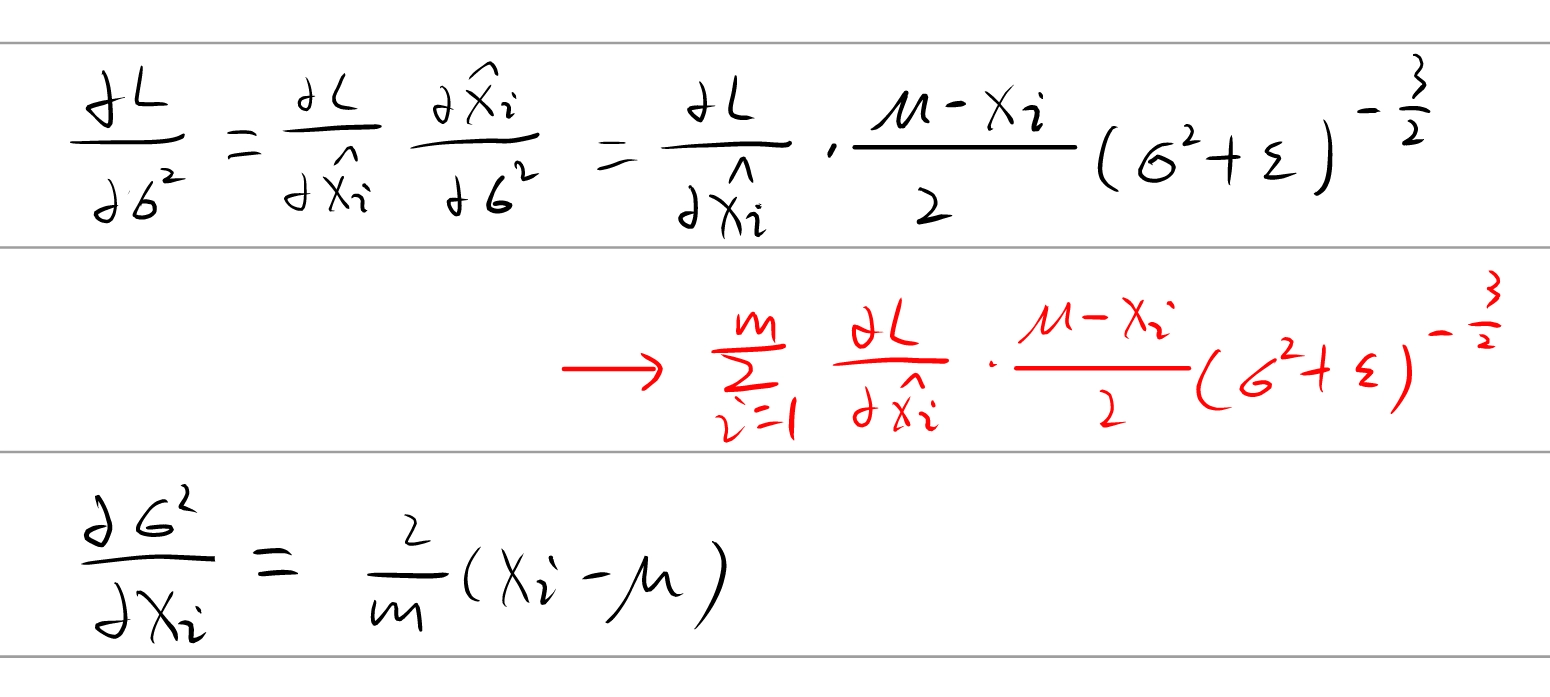该文章距离上次编辑已经过了 699 天, 文章内容可能已过期，请仔细甄别

随机梯度下降法 SGD

stochastic gradient descent

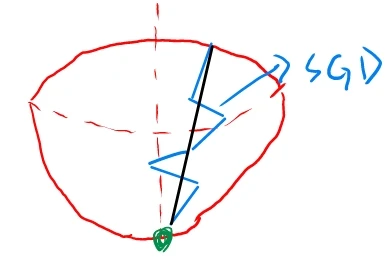
假设红色部分为一个下凹空间，现在要前往空间的最低点。随机梯度下降法 SGD 低效的根本问题在于，每一步虽然都是立足于当前点的梯度方向（蓝线），但梯度的方向并不一定指向最小值的方向（黑线）。

Screenshot_2023-06-08-20-07-55-817_com.newskyer.d.jpg

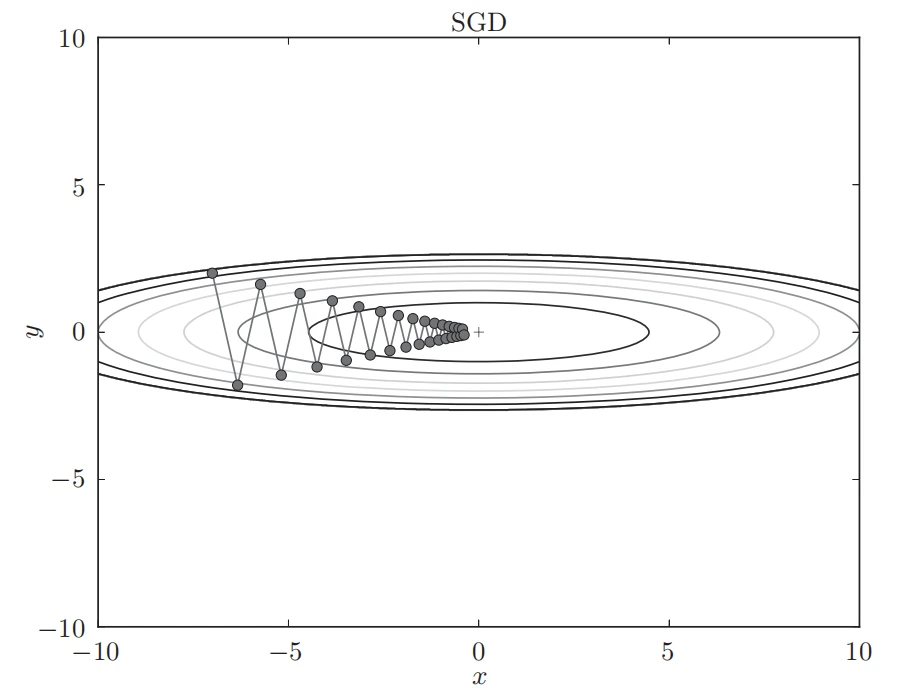
image.png

基于SGD的最优化的更新路径：呈“之”字形朝最小值(0, 0)移动，效率低

python
1
2
3
4
5
6
7
8
9
10
class SGD:

    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

Momentum

数学式表示

v←αv−η∂L∂WW←W+v\begin{align} v & \leftarrow \alpha v - \eta \frac{\partial L}{\partial W} \\ W & \leftarrow W + v \end{align}

WW 为要更新的权重参数， ∂L∂W\frac{\partial L}{\partial W} 表示损失函数关于 WW 的梯度， η\eta 表示学习率， vv 对应物理上的速度。

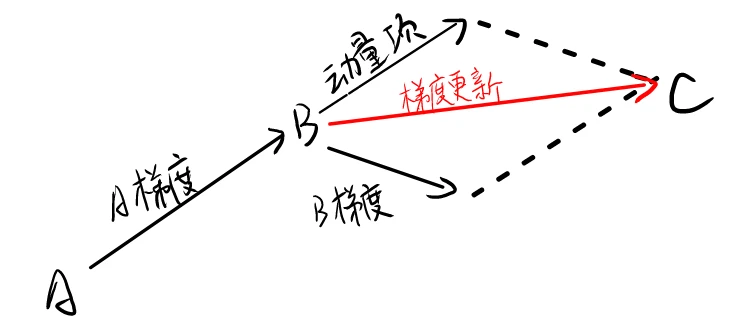
Screenshot_2023-06-08-21-27-57-372_com.newskyer.d.png

当从 A 点沿梯度方向走到 B 点时，将 B 的梯度方向与动量项合并，作为新的更新方向

  1. 如果 B 点梯度方向不变，由于加上了动量项，可以使 SGD 加快更新
  2. 如果 B 点梯度方向改变，动量项可以减弱更新幅度，防止发生较大改变导致更新不稳定

image.png

基于 Momentum 的最优化的更新路径

和 SGD 相比，我们发现“之”字形的“程度”减轻了。这是因为虽然 x 轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。

反过来，虽然 y 轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以 y 轴方向上的速度不稳定。因此，和 SGD 时的情形相比，可以更快地朝 x 轴方向靠近，减弱“之”字形的变动程度。

代码

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

AdaGrad

自适应地为各个维度的参数分配不同的学习率

在神经网络的学习中，学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。

在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。AdaGrad（Ada 意为 Adaptive）会为参数的每个元素适当地调整学习率，与此同时进行学习。

h←h+∂L∂W⊙∂L∂WW←W−η1h+ϵ∂L∂W\begin{align} h & \leftarrow h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W} \\ W & \leftarrow W - \eta \frac1{\sqrt{h+\epsilon}} \frac{\partial L}{\partial W} \end{align}

hh 保存了以前的所有梯度值的平方和， ⊙\odot 表示 element-wise 矩阵乘法（对应位置元素相乘）， ϵ\epsilon 是一个极小值，防止出现分母为 0 的情况。

  • 优点：h 较小时，可以放大梯度；较大时，可以约束梯度（奖励+惩罚）
  • 缺点：
    • 梯度累积导致学习率单调递减，后期学习率极小
    • 仍然需要设置一个合适的全局初始学习率

代码

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class AdaGrad:

    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            # 分母不得为0，加1e-7极小值
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

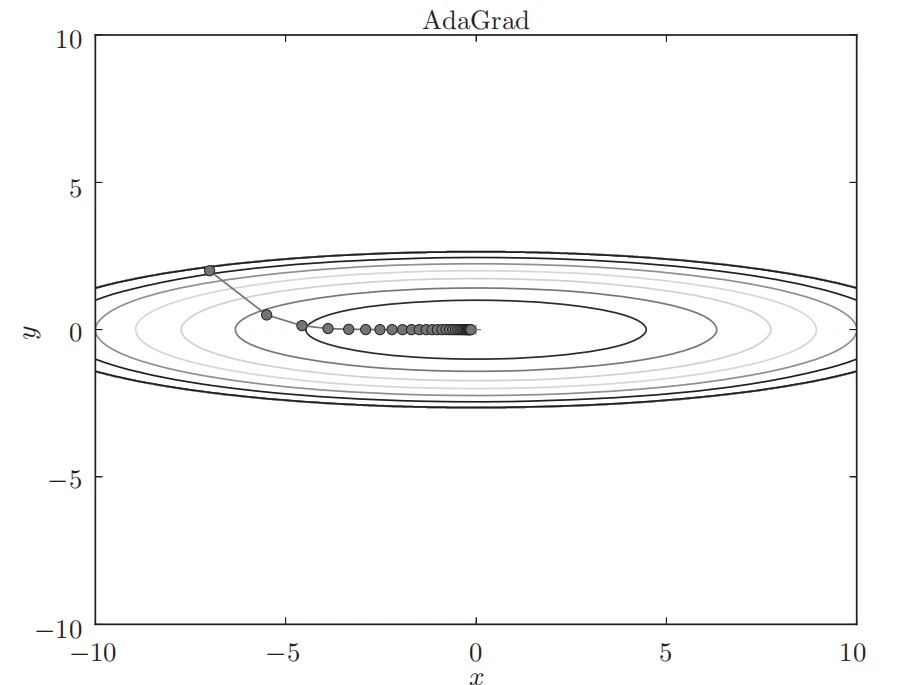
image.png

基于 AdaGrad 的最优化的更新路径

RMSProp

在 AdaGrad 基础上产生的改进版

Gt=βGt−1+(1−β)gt2△θt=−ηGt+ϵgt\begin{align} G_t = \textcolor{red}{\beta} G_{t-1} + \textcolor{red}{ (1-\beta) } g_t^2 \\ \vartriangle \theta_t = - \frac \eta {G_t + \epsilon} g_t \end{align}

其中， β\beta 默认为 0.9。

可以看见，RMSProp 与 AdaGrad 不同，它通过增加一个衰减系数，只关注最近某一时间窗口内的下降梯度，来控制历史梯度信息的获取。

​ GtG_t 是由历史平方梯度和当前平方梯度加权得到的平均数，而 β\beta 控制了历史平方梯度的权重：

  • 当 β\beta 较小时，平均数会对历史梯度进行平滑，从而减少历史梯度对参数更新的影响；
  • 当 β\beta 较大时，平均数会对历史梯度进行加权平均，从而增加历史梯度对参数更新的影响。

因此可以在一定程度上缓解 AdaGrad 在后期学习率太小这个问题。

代码

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class RMSprop:

    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        # 衰减系数
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

Adam

Momentum + RMSProp = Adam

image.png

Adam 采用两个不同的超参数 β1 和 β2 来控制动量以及 RMSProp 中指数加权移动平均 sts_t 的更新。

mt=β1⋅mt−1+(1−β1)⋅gtvt=β2⋅vt−1+(1−β2)⋅(gt⊙gt)θt=θt−1−η⋅mt^vt^+ϵ\begin{align} m_t & = β_1 · m_{t-1} + (1 - β_1) · g_t \\ v_t & = β_2 · v_{t-1} + (1 - β_2) · (g_t⊙g_t) \\ \theta_t & = \theta_{t-1} - \frac {\eta \cdot \hat{m_t}} { \sqrt{\hat{v_t}} + \epsilon} \end{align}

通常，β1=0.9，β2=0.999，ϵ=1e−7

初始化偏差修正

Adam 的一个改进点是 Adam 对一阶矩估计和二阶矩估计进行了修正，使其近似为对期望的无偏估计。修正方式为：

mt^=mt1−β1tvt^=vt1−β2t\begin{align} \hat{m_t} = \frac {m_t} {1-\beta_1^t} \\ \hat{v_t} = \frac {v_t} {1-\beta_2^t} \end{align}

下面对偏差修正进行解释。

通过下列推导得到在前面所有时间步上只包含梯度和衰减率的函数，即消去 v：

Screenshot_2023-06-09-11-26-29-585_com.newskyer.d.png

image.png

E (aX) = aE (X)，好像是有这么个期望公式？概率论忘干净了 hhhh

Screenshot_2023-06-09-11-35-35-472_com.newskyer.d.png

可以发现，当 t 取的很小时，例如 t=1，此时 v1=0.001g12v_1 = 0.001g_1^2 。显然，在迭代初期，这个偏差很大，因此需要对其作出修正，即 vt^=vt1−β2t\hat{v_t} = \frac {v_t} {1-\beta_2^t} 。如此一来，当 t 取的很小时，可以起到放大的效果来修正偏差；当 t 足够大时， vt^≈vt\hat{v_t} \approx v_t ，即偏差修正几乎没有作用。

对一阶动量的修正也是同理

代码

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
        
        for key in params.keys():
            self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

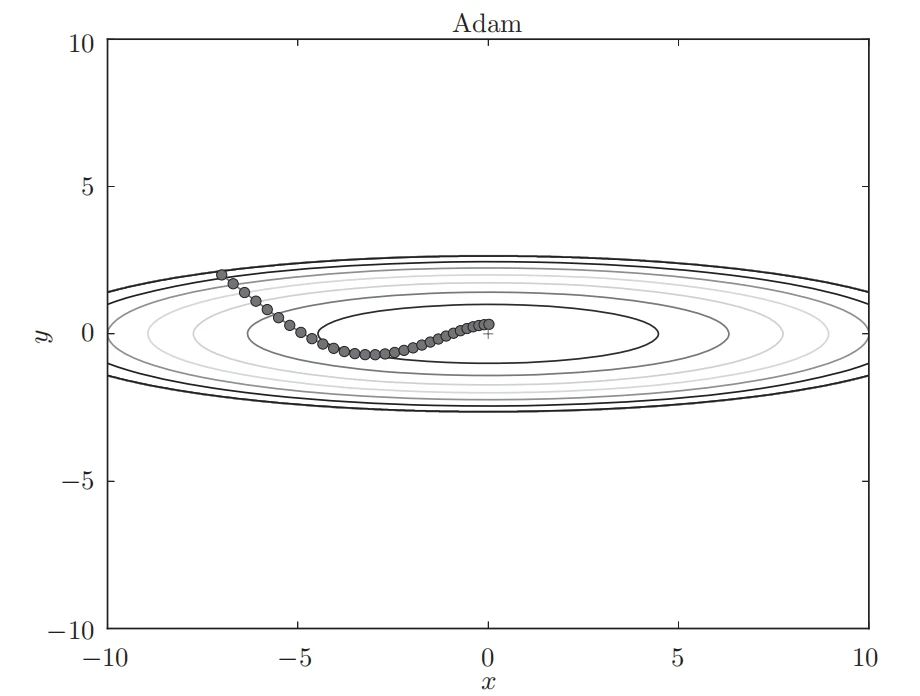
image.png

基于 Adam 的最优化的更新路径

虽然 Momentun 也有类似的移动，但是相比之下，Adam 的 y 轴震荡程度有所减轻，这得益于学习的更新程度被适当地调整了。

对比

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import matplotlib.pyplot as plt
from d2l.mnist import load_mnist
from d2l.common.util import smooth_curve
from d2l.common.multi_layer_net import MultiLayerNet
from d2l.common.optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

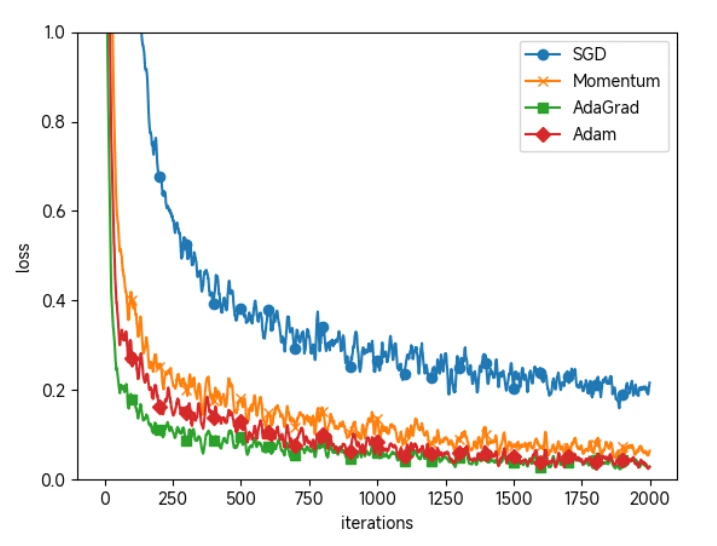
image.png

基于 MNIST 数据集的4种更新方法的比较：横轴表示学习的迭代次数（iteration），纵轴表示损失函数的值（loss）

权重的初始值

初始权重可以为 0 吗

将权重初始值设为 0 的话，将无法正确进行学习。严格地说，不能将权重初始值设成一样的值。因为在误差反向传播法中，所有的权重值都会进行相同的更新，因此，权重被更新为相同的值，并拥有了对称的值（重复的值）。

这使得神经网络拥有许多不同的权重的意义丧失了。为了防止“权重均一化”（严格地讲，是为了瓦解权重的对称结构），必须随机生成初始值。

隐藏层的激活值分布

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def ReLU(x):
    return np.maximum(0, x)


def tanh(x):
    return np.tanh(x)

# 随机生成一个元素符合标准正态分布（高斯分布）的数组作为输入层
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    # 如果不是第一层，将前一层输出作为本层输入
    if i != 0:
        x = activations[i-1]

    # 重新生成一个100x100的高斯分布数组作为本层权重
    w = np.random.randn(node_num, node_num) * 1
    
    a = np.dot(x, w)

    # 激活后获得本层输出
    z = sigmoid(a)

    # 保存本层输出，以便下一层使用
    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    # 按层数划分子图
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    # 非输入层，隐藏y轴上的刻度标签和刻度线
    if i != 0:
        plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    # 绘制直方图：a扁平化，直方图30条，统计(0,1)间的数据
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

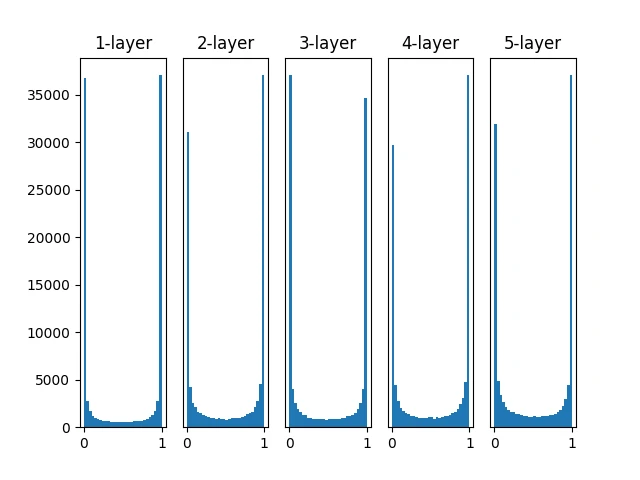
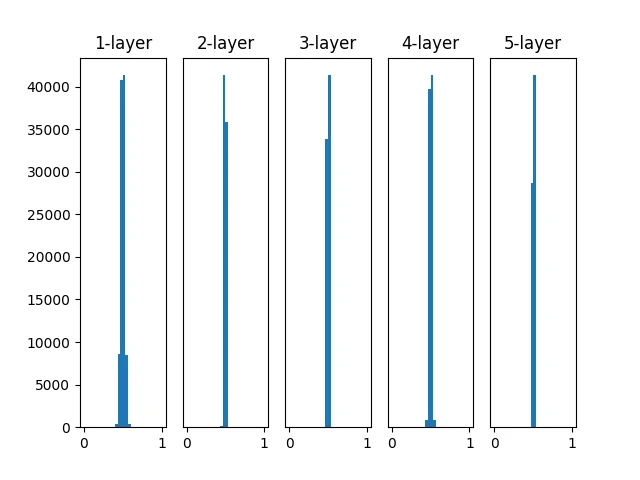
通过上述代码我们可以得到如下的数据分布图。其记载了一个 5 层神经网络，每层有 100 个神经元，激活函数使用 sigmoid，传入标准正态分布随机生成的数据后，用直方图绘制各层激活值的数据分布。

image.png

如上图，各层的激活值呈现偏向 0 和 1 的分布

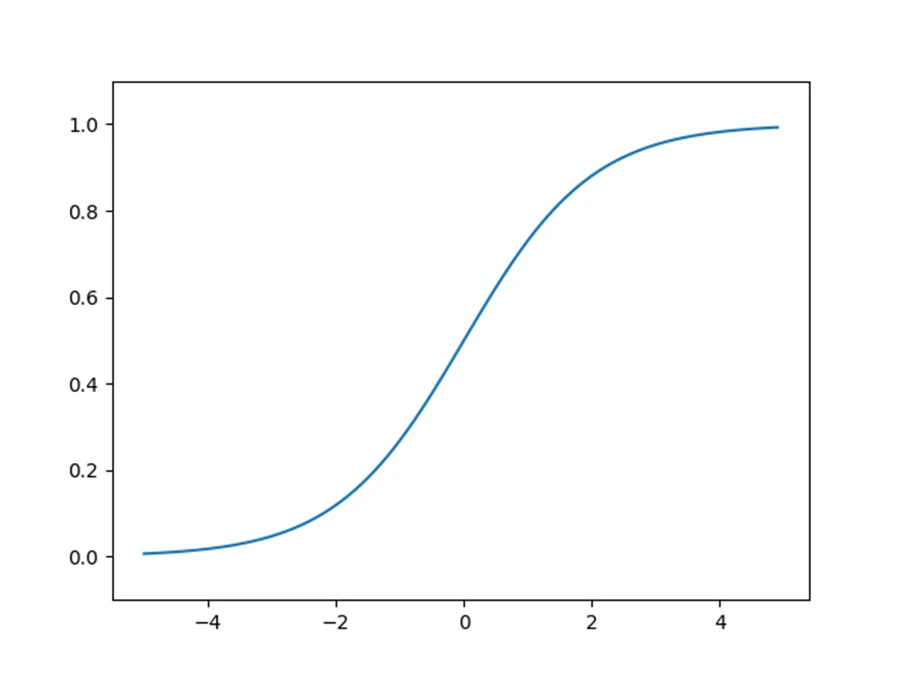
image.png

这是 sigmoid 函数的图像，可见它是一个 S 型函数，随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接近0。因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。

那如果将高斯分布的标准差设为 0.01 呢？

python
1
w = np.random.randn(node_num, node_num) * 0.01

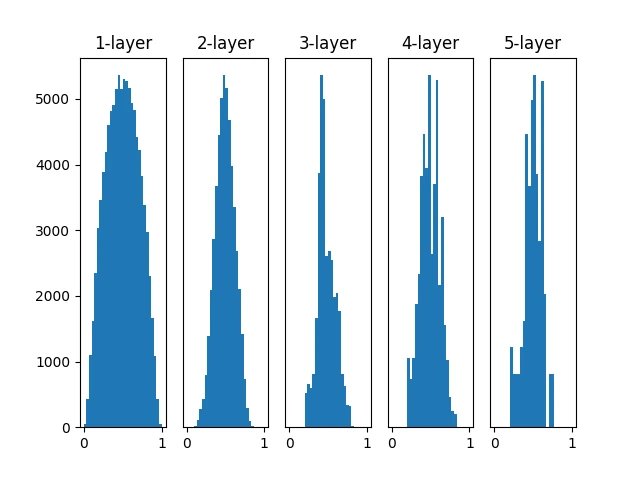
image.png

这次呈集中在0.5附近的分布。因为不像刚才的例子那样偏向0和1，所以不会发生梯度消失的问题。但是，激活值的分布有所偏向，说明在表现力上会有很大问题。

因为如果有多个神经元都输出几乎相同的值，那它们就没有存在的意义了。比如，如果100 个神经元都输出几乎相同的值，那么也可以由1个神经元来表达基本相同的事情。因此，激活值在分布上有所偏向会出现“表现力受限”的问题。

Xavier 初始值

Xavier Glorot 等人在论文中推荐了一种权重初始值，俗称“Xavier 初始值”。现在，在一般的深度学习框架中，Xavier 初始值已被作为标准使用。其推导出的结论是，如果前一层的节点数为 n，则初始值使用标准差为 1n\frac1{\sqrt{n}} 的分布。

显然，前一层节点数越多，n 越大，则方差越小，因此初始值的尺度就越小

[!warning]
Xavier 初始值是以激活函数是线性函数为前提推导出的

将上文代码中的权重改为

python
1
w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)

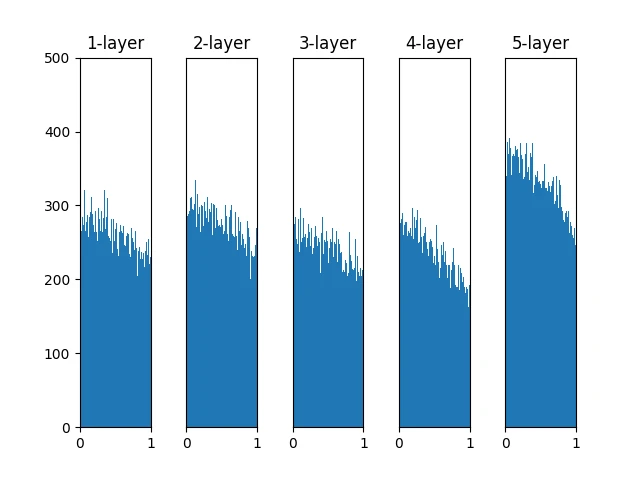
image.png

越是后面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。因为各层间传递的数据有适当的广度，所以 sigmoid 函数的表现力不受限制，有望进行高效的学习。

[!tip]
用作激活函数的函数最好具有关于原点对称的性质

ReLU 的权重初始值

当激活函数使用 ReLU 时，一般推荐使用 ReLU 专用的初始值，也就是 Kaiming He 等人推荐的初始值，也称为 “He 初始值”。

当前一层的节点数为 n 时，He 初始值使用标准差为 2n\sqrt{\frac2{n}} 的高斯分布。

可以理解为，因为 ReLU 函数值域为非负数，因此为了使其具有更大的广度，需要使用 Xavier 初始值的 2 倍（更大的方差，更大的尺度）

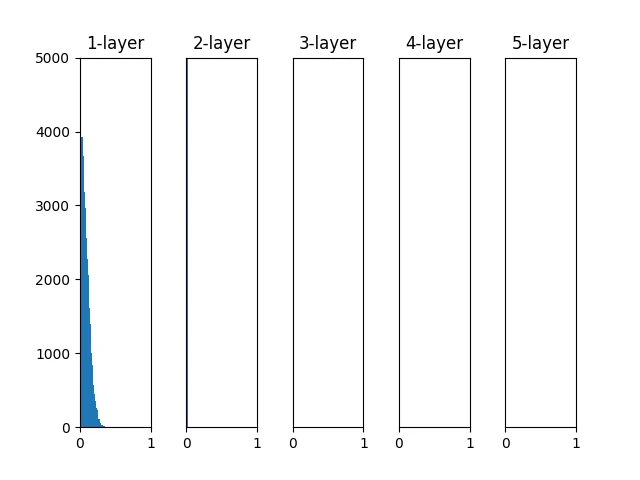
image.png

权重初始值为标准差是 0.01 的高斯分布时

神经网络上传递的是非常小的值，说明逆向传播时权重的梯度也同样很小。这是很严重的问题，实际上学习基本上没有进展。

image.png

权重初始值为 Xavier 初始值时

随着层的加深，偏向一点点变大。实际上，层加深后，激活值的偏向变大，学习时会出现梯即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。度消失的问题。

image.png

权重初始值为 He 初始值时

即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

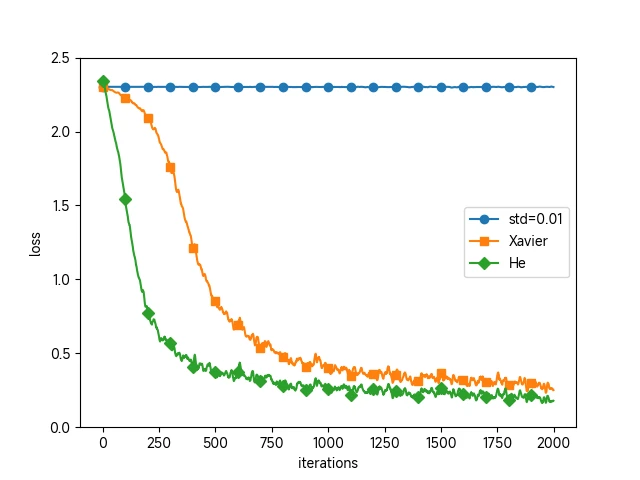
基于 mnist 数据集的权重初始值比较

image.png

  • 标准差为 0.01 的正态分布压根没法学习，损失函数动都不动
  • Xavier 和 He 效果很好，且 He 学习进度更快（loss 下降的更快）

Batch Normalization

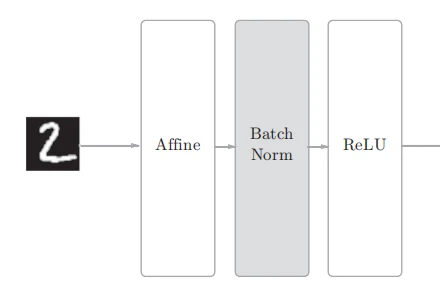
Batch Normalization（批量归一化） 的思路是调整各层的激活值分布使其拥有适当的广度, 因此在 affine 层与 ReLU 层之间添加一个 Batch Norm 层以对神经网络中的数据进行正规化。

image.png

其具体操作如下

μB←1m∑i=1mxiσB2←1m∑i=1m(xi−μB)2xi^←xi−μBσB2+ϵ\begin{align} \mu_B & \leftarrow \frac1m \sum_{i=1}^m x_i \\ \sigma_B^2 & \leftarrow \frac1m \sum_{i=1}^m (x_i - \mu_B)^2 \\ \hat{x_i} & \leftarrow \frac{x_i - \mu_B}{ \sqrt{\sigma_B^2 + \epsilon} } \end{align}

这里对 mini-batch 的 m 歌输入数据的集合 {x1,x2,...,xm}\{x_1, x_2, ..., x_m\} 分别求均值 μB\mu_B 和方差 σB2\sigma_B^2 ，然后更新 xix_i ，将其正规化为均值为 0，方差为 1 的数据 {x1,x2,...,xm^}\{\hat{x_1, x_2, ..., x_m}\} ,以此来减小数据分布的倾向。ϵ\epsilon 为极小值，防止出现除 0。

接着，Batch Norm 层会对正规化后的数据进行缩放和平移的变换，用数学式可以如下表示

yi←γxi^+βy_i \leftarrow \gamma \hat{x_i} + \beta

这里， γ\gamma 和 β\beta 是参数。一开始 γ=0\gamma = 0 ， β=1\beta = 1 （因为这些值可以保持输出的原始分布）后经过学习调整为合适的值。

推导过程详解

  • 反向传播初始梯度为 ∂L∂yi\frac {\partial L} {\partial{y_i}}
  • 需要计算 ∂L∂xi\frac {\partial L} {\partial{x_i}} ， ∂L∂γ\frac {\partial L} {\partial \gamma} ， ∂L∂β\frac {\partial L} {\partial \beta}

Screenshot_2023-06-10-13-24-59-958_com.newskyer.d.png

Screenshot_2023-06-10-13-25-12-733_com.newskyer.d.png

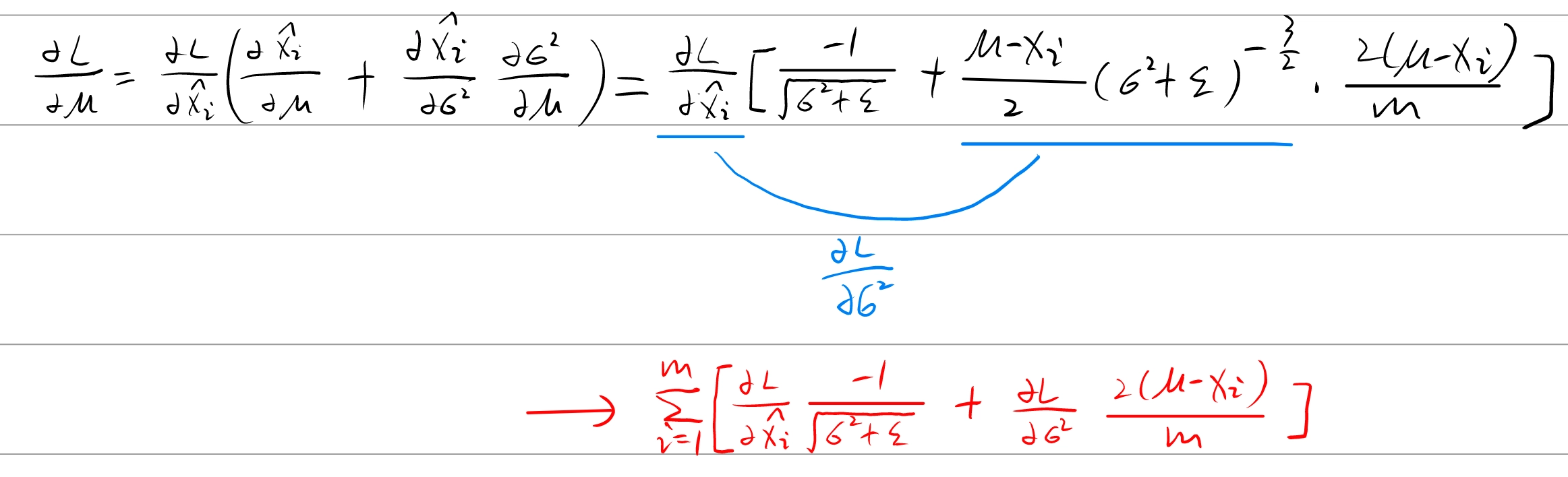
论文中，作者将 ∂L∂xi\frac {\partial L} {\partial{x_i}} 拆分为如下三个部分

∂L∂xi=∂L∂xi^∂xi^∂xi+∂L∂σ2∂σ2∂xi+∂L∂μ∂μ∂xi\frac {\partial L} {\partial{x_i}} = \frac {\partial L} {\partial{\hat{x_i}}} \frac {\partial \hat{x_i}} {\partial{x_i}} + \frac {\partial L} {\partial{\sigma^2}} \frac {\partial \sigma^2} {\partial{x_i}} + \frac {\partial L} {\partial{\mu}}\frac {\partial \mu} {\partial{x_i}}

下面是它们的推导过程

Screenshot_2023-06-10-13-19-10-458_com.newskyer.d.png

Screenshot_2023-06-10-13-19-23-721_com.newskyer.d.png

Screenshot_2023-06-10-13-19-40-642_com.newskyer.d.png

这里漏写了一个， ∂μ∂xi=1m\frac {\partial \mu} {\partial x_i} = \frac 1 m

论文原文
image.png

过拟合

发生过拟合的原因，主要有以下两个。

  • 模型拥有大量参数、表现力强
  • 训练数据少

例如从 MNIST 数据集原本的6w个训练数据中只选定300个

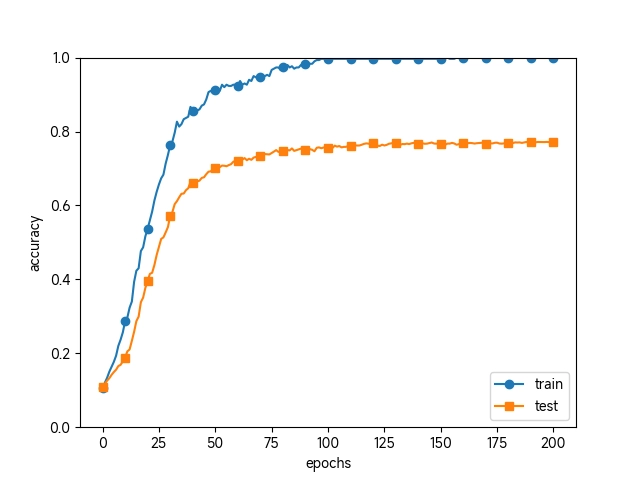
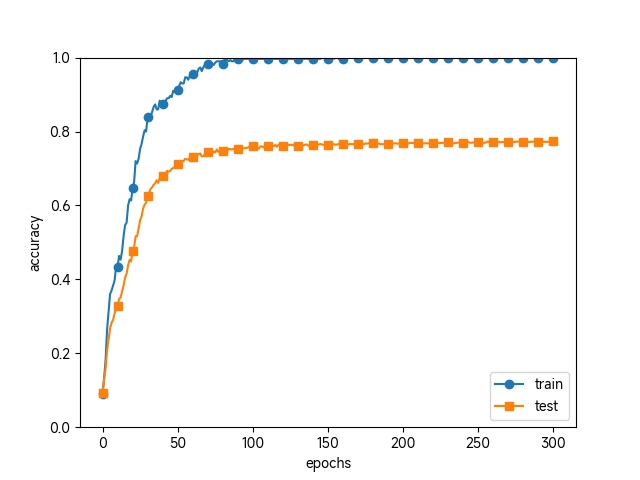
image.png

不使用权值衰减

过了 100 个 epoch 左右后，用训练数据测量到的识别精度几乎都为 100%。但是，对于测试数据，离 100% 的识别精度还有较大的差距。如此大的识别精度差距，是只拟合了训练数据的结果。从图中可知，模型对训练时没有使用的一般数据（测试数据）拟合得不是很好。

权值衰减

权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

如果权值为 WW ，则为损失函数加上权重的平方范数（L2范数），即 12λW2\frac12 \lambda W^2 。因此，在求权重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数 λW\lambda W

  • λ\lambda 是控制正则化强度的超参数，设置得越大，对大的权重施加的惩罚就越重。
  • 12\frac12 是为了 12λW2\frac12 \lambda W^2 的求导结果变为 λW\lambda W 而使用的调整常量
python
1
2
3
4
5
6
7
8
9
10
11
def loss(self, x, t):

    y = self.predict(x)

    weight_decay = 0
    for idx in range(1, self.hidden_layer_num + 2):
        W = self.params['W' + str(idx)]
        # 权重衰减项会在每次更新时被累加，以确保越来越多的权重被惩罚
        weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)

    return self.last_layer.forward(y, t) + weight_decay

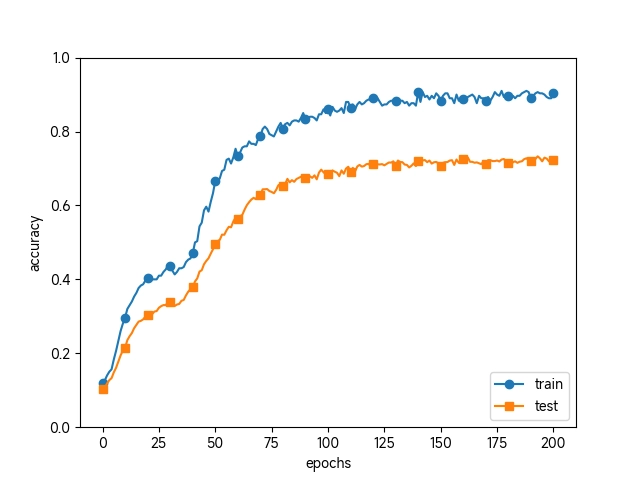
image.png

使用了权值衰减

虽然训练数据的识别精度和测试数据的识别精度之间有差距，但是与没有使用权值衰减的结果相比，差距变小了。这说明过拟合受到了抑制。

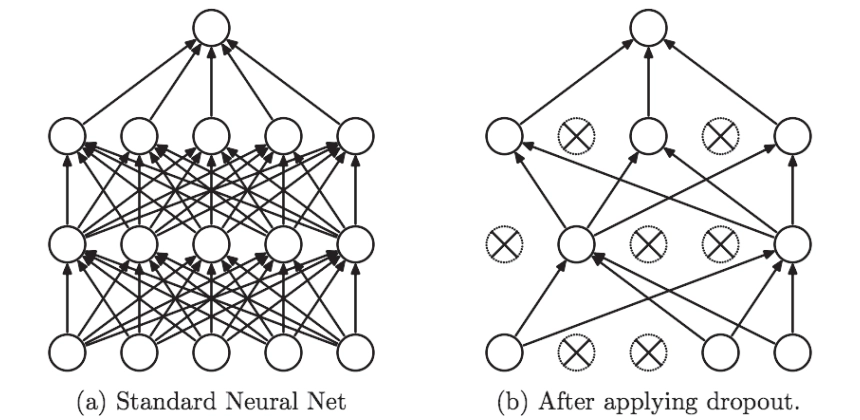
Dropout

Dropout 是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

image.png

不听话？不听话就夹你！

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Dropout:

    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            # 生成的同型数组中，大于ratio的置为True，否则为False
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            # 与x相乘后，为True的保留，为False的被置为0，达到drop节点的作用
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        # 反向传播时，行为与ReLU相同，即  
        # 正向传播时传递了信号的神经元，反向传播时按原样传递信号  
        # 正向传播时没有传递信号的，反向传播时信号将停在那里
        return dout * self.mask

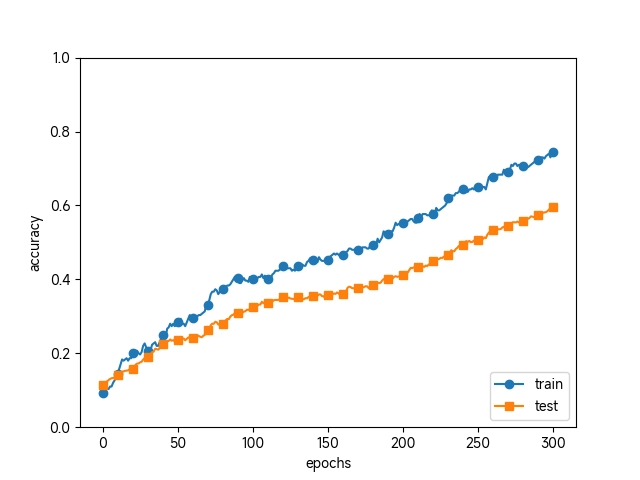
image.png

没有使用 Dropout

image.png

使用了 Dropout

通过使用 Dropout，即便是表现力强的网络，也可以抑制过拟合。

机器学习中经常使用集成学习。所谓集成学习，就是让多个模型单独进行学习，推理时再取多个模型的输出的平均值。

用神经网络的语境来说，比如，准备 5个结构相同（或者类似）的网络，分别进行学习，测试时，以这 5个网络的输出的平均值作为答案。实验告诉我们，通过进行集成学习，神经网络的识别精度可以提高好几个百分点。

这个集成学习与 Dropout 有密切的关系。这是因为可以将 Dropout 理解为，通过在学习过程中随机删除神经元，从而每一次都让不同的模型进行学习。并且，推理时，通过对神经元的输出乘以删除比例（比如，0.5等），可以取得模型的平均值。也就是说，可以理解成，Dropout 将集成学习的效果（模拟地）通过一个网络实现了。

超参数

超参数是指，比如各层的神经元数量、batch 大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值，模型的性能就会很差。

调整超参数时，必须使用超参数专用的确认数据，一般称为验证数据（validation data）。我们使用这个验证数据来评估超参数的好坏。比较理想的是只用一次验证数据。

[!warning]
不能使用测试数据评估超参数的性能，否则超参数的值会对测试数据发生过拟合！

根据不同的数据集，有的会事先分成训练数据、验证数据、测试数据三部分，有的只分成训练数据和测试数据两部分，有的则不进行分割。在这种情况下，用户需要自行进行分割。例如用训练数据的20%作为验证数据。

python
1
2
3
4
5
6
7
8
9
10
def shuffle_dataset(x, t):
    """
    打乱数据集
    """
    # 随机排列一个数组或者一个整数范围内的数。它返回一个新的、随机排列的数组
    permutation = np.random.permutation(x.shape[0])
    x = x[permutation, :] if x.ndim == 2 else x[permutation, :, :, :]
    t = t[permutation]

    return x, t

超参数的范围只要 “大致地指定” 就可以了。所谓“大致地指定”，是指像0.001（ 10−310^{−3} ）到1000（ 10310^3 ）这样，以“10的阶乘”的尺度指定范围，也表述为“用对数尺度（log scale）指定”。

python
1
2
3
4
# 指定搜索的超参数的范围
# 生成一个在区间 [-8, -4) 内均匀分布的随机浮点数
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)

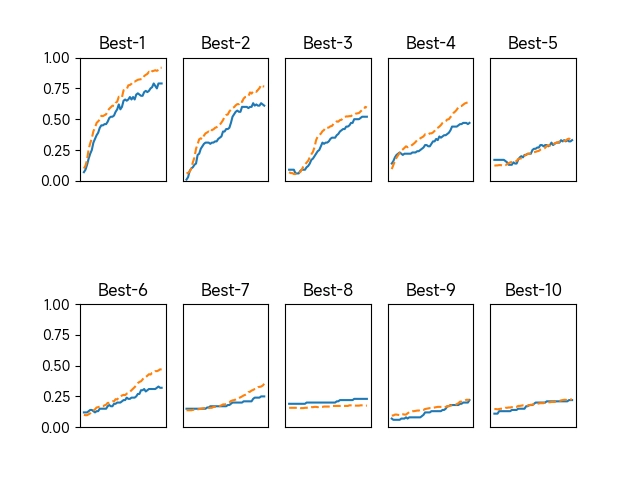
在超参数的最优化中，要注意的是深度学习需要很长时间（比如，几天或几周）。因此，在超参数的搜索中，需要尽早放弃那些不符合逻辑的超参数。于是，在超参数的最优化中，减少学习的 epoch，缩短一次评估所需的时间是一个不错的办法。

plaintext
1
2
3
4
5
6
7
Best-1(val acc:0.79) | lr:0.008381149872316536, weight decay:1.2740132675595203e-07
Best-2(val acc:0.61) | lr:0.006798932859815733, weight decay:5.427724799985068e-05
Best-3(val acc:0.52) | lr:0.003081830866896804, weight decay:3.424534700612302e-06
Best-4(val acc:0.47) | lr:0.003997839005016555, weight decay:1.3090155201683637e-06
Best-5(val acc:0.33) | lr:0.001760154887955398, weight decay:6.227114725290454e-07
Best-6(val acc:0.32) | lr:0.002993807782496189, weight decay:7.564414060749376e-07
Best-7(val acc:0.25) | lr:0.0018178836880097615, weight decay:1.4716823735556433e-05

例如一次训练后，我们发现学习率在0.001到0.01，权值衰减系数在 10−710^{-7} 到 10−510^{-5} 之间时，学习效果不错。因此，在这个缩小的范围中重复相同的操作，这样就能缩小到合适的超参数的存在范围，然后在某个阶段，选择一个最终的超参数的值。

image.png