算法-回溯算法

n 后问题

问题定义

在 $n \times n$ 格的棋盘上放置彼此不受攻击的 $n$ 个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 $n$ 后问题等价于在 $n \times n$ 格的棋盘上放置 $n$ 个皇后，任何 2 个皇后不放在同一行或同一列或同一斜线上。

算法思想

用 $n$ 元组 $x[1:n]$ 表示 $n$ 后问题的解。其中， $x[i]$ 表示皇后 $i$ 放在第 $i$ 行的第 $x[i]$ 列，则存在以下要求：

不在同一行： $i$ 不同就可以保证
不在同一列： $x[i]$ 表示第 $x[i]$ 列，因此 $x[i]$ 也互不相同

[!info] 对于不在同一斜线的情况，做出以下论述。

假设 $n \times n$ 格的棋盘的行号从左到右、列号从上到下分别为 $1,2,...,n$ ，则：

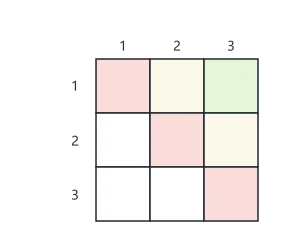
斜率为 $-1$ 的直线（有若干条，且互相平行）所对应的格子，例如下图中黄色方格的坐标分别为 $(1,2),\ (2,3)$ ，其横纵坐标的差值都为 $-1$ 。同理，红色、黄色对应方格的坐标差值 $0$ 和 $-2$ ，也是分别相同的。

因此，假设两个皇后放置的位置分别为 $(i,j),\ (k,l)$ ，若 $i-j=k-l$ ，则说明两者同处于斜率为 $-1$ 的斜线上。
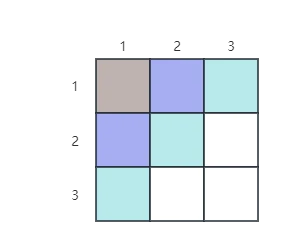
斜率为 $+1$ 的直线所对应的格子，例如下图中宇宙超级无敌绝绝魅惑紫色方格的坐标分别为 $(2,1),\ (1,2)$ ，其横纵坐标的和都为 $3$ 。同理，青色与褐色对应的方格的坐标和也是分别相同的。

因此，假设两个皇后放置的位置分别为 $(i,j),\ (k,l)$ ，若 $i+j=k+l$ ，则说明两者同处于斜率为 $+1$ 的斜线上。

综上所述，我们可以给出 N 后问题的所有约束。

代码实现

[!info] 关于 N 后问题，有一个未按照上述思路优化的原始版本，见仓库代码 NQueen.c

/**
 * 判断在指定位置放置皇后是否可行
 *
 * @param solution 存放皇后位置的数组
 * @param row      当前行数
 * @param col      当前列数
 * @return         如果安全放置皇后，则返回 true；否则返回 false
 */
bool isSafe(int* solution, int row, int col) {
    for (int i = 0; i < row; i++) {
        // 检查是否在同一列或同一斜线上
        if (solution[i] == col || abs(i - row) == abs(solution[i] - col)) {
            return false;
        }
    }
    return true;
}

/**
 * 解决N皇后问题的辅助函数
 * 
 * @param solution 存放皇后位置的数组
 * @param row 当前处理的行
 * @param n 皇后的数量
 */
void solveNQueensUtil(int* solution, int row, int n) {
    if (row == n) {
        // 处理完最后一行，表示找到一个解
        printSolution(solution, n);
        return;
    }

    for (int col = 0; col < n; col++) {  // 遍历当前行的每一列
        if (isSafe(solution, row, col)) {
            // 当前位置安全，将皇后放置在该位置
            solution[row] = col;

            // 递归地尝试放置下一行的皇后
            solveNQueensUtil(solution, row + 1, n);

            // 没有显式地撤销当前皇后的位置，这是因为我们使用了一个一维数组 solution 来存储每行皇后的列位置
            // 回溯：当递归返回到当前行时，我们会继续在其他列尝试放置皇后。在这个过程中，solution[row] 的值会被新的列位置覆盖，这实际上就是撤销了之前放置在该行的皇后。

        }
    }
}

/**
 * 解决N皇后问题
 * 
 * @param n 皇后的数量
 */
void solveNQueens(int n) {
    int* solution = (int*)malloc(n * sizeof(int));  // 申请分配用于存放皇后位置的数组

    solveNQueensUtil(solution, 0, n);  // 从第0行开始处理

    free(solution);  // 释放内存
}

[!question] 为什么 isSafe() 中检查冲突时，只需要检查前 row 行？

在 N 后问题中，我们通常会按行顺序，每一次放置一个皇后。也就是说，当我们在检查是否可以在第 row 行和第 col 列放置皇后时，我们知道所有在第 row 行之前的行已经放置了皇后，而所有在第 row 行之后的行还没有放置皇后。

01 背包问题

问题定义

01 背包问题是背包问题的一个特例，即装入物品时，不能装入物品的一部分，要么全部装入、要么不装入，因为这种非此即彼的选择方式，得名 01 背包问题。

算法思想

在背包问题的解决过程中，我们需要尝试所有可能的物品组合，以找到最优解。为了实现这一点，我们对每个物品都有两种选择：选择它或者不选择它，分别对应解空间的左右子树。当我们选择了一个物品（即 selected[index] = true;）并递归地处理了所有后续的物品后，我们需要撤销对当前物品的选择，以便我们可以在不选择当前物品的情况下，尝试所有可能的后续选择。

但是，当不选择当前物品时，我们可以借助剪枝函数提前回溯：若不选择当前物品 index，则假设尽力装入从下一物品 index+1 开始的剩余物品（按背包问题的方式，即可以装入部分），可以求出一个价值上界。那么：

如果这个价值上界小于当前的最高价值，则无需继续考虑从 index+1 开始的该分枝。原因很简单，你 TM 把剩下的破玩意都塞进去也不能达到新的最大价值，那我还装你干什么。
反之，如果这个价值上界大于当前的最高价值，那才有考虑该分枝的价值。

代码实现

// 定义物品结构体
typedef struct {
    int id;
    int weight;
    int value;
} Item;

/**
 * 计算选择剩余所有物品后的价值上界
 * 
 * @details 用于剪枝，如果价值上界小于当前最大价值，则不再继续搜索
 * 
 * @param items 物品数组
 * @param n 物品数量
 * @param W 背包容量
 * @param index 当前物品索引
 * @param currentWeight 当前背包重量
 * @param currentValue 当前背包价值
 * @return 价值上界
 */
int upperBound(Item* items, int n, int W, int index, int currentWeight, int currentValue) {
    int remainingWeight = W - currentWeight;  // 剩余容量
    int upperValue = currentValue;  // 上界价值：初始值为当前已选中物品的总价值

    // 从index开始，尽可能多地装入物品
    while (index < n && items[index].weight <= remainingWeight) {  // 不是最后一个物品，且剩余容量足够装下当前物品
        remainingWeight -= items[index].weight;
        upperValue += items[index].value;
        index++;
    }

    if (index < n) {  // 剩余容量不足以装下当前物品
        upperValue += (remainingWeight * (items[index].value/items[index].weight));  // 装入部分当前物品，更新上界价值
    }

    return upperValue;
}

/**
 * 回溯搜索函数
 *
 * @param items 物品数组
 * @param n 物品数量
 * @param W 背包容量
 * @param selected 选中的物品数组
 * @param currentWeight 当前背包重量
 * @param currentValue 当前背包价值
 * @param maxValue 最大背包价值
 * @param index 当前物品索引
 */
void backtrack(Item* items, int n, int W, bool* selected, int* currentWeight, int* currentValue, int* maxValue, int index) {
    if (index == n) {  // 处理完所有物品
        if (*currentWeight <= W && *currentValue > *maxValue) {  // 找到一个更优解
            *maxValue = *currentValue;
            printf("The max value is: %d\n", *maxValue);
            printf("The best choice is as follows:\n");
            for (int i = 0; i < n; i++) {
                if (selected[i]) {
                    printf("item %d\n", items[i].id);
                }
            }
            printf("----------\n");
        }
        return;
    }

    if (*currentWeight + items[index].weight <= W) {  // 当前物品可以装入背包
        selected[index] = true;  // 选中当前物品
        // 更新当前总重量和总价值
        *currentWeight += items[index].weight;
        *currentValue += items[index].value;
        // 选择当前物品的情况下，递归处理下一个物品
        backtrack(items, n, W, selected, currentWeight, currentValue, maxValue, index + 1);

        selected[index] = false;  // 撤销选择当前的物品
        // 恢复不选择这个物品时的总重量和总价值
        *currentWeight -= items[index].weight;
        *currentValue -= items[index].value;
    }
    
    // 不选择当前物品(从index+1开始)的情况下，尝试所有可能的后续选择
    // 如果选择剩余物品的上界价值大于当前最大价值，则递归处理下一个物品
    if (upperBound(items, n, W, index + 1, *currentWeight, *currentValue) > *maxValue) {
        backtrack(items, n, W, selected, currentWeight, currentValue, maxValue, index + 1);  
    }
}

/**
 * 解决01背包问题
 * 
 * @param items 物品数组
 * @param n 物品数量
 * @param W 背包容量
 */
void knapsack(Item* items, int n, int W) {
    // 初始化
    bool selected[n];
    int currentWeight = 0;
    int currentValue = 0;
    int maxValue = 0;
    int index = 0;

    // 按照单位重量价值进行降序排序
    qsort(items, n, sizeof(Item), compare);
    printf("Sort by unitValue:\n");
    for (int i = 0; i < n; i++)
    {
        printf("item %d: weight = %d, value = %d, unitValue = %d\n", items[i].id, items[i].weight, items[i].value, items[i].value/items[i].weight);
    }
    printf("----------\n");
    

    backtrack(items, n, W, selected, &currentWeight, &currentValue, &maxValue, index);

    printf("The final best value is: %d\n", maxValue);
}